今回医師国家試験が終わり暇だったので2021京大理系数学の問題を自力で解いてみました。
その模様をYoutube にあげていたのですが、一応解答を確認したところ少なくとも解答の数字は正しそうなので受験生でもし解答を早く確認したいという方がいましたら参考にして頂ければと思います。
大問1 問1(13/9,5/9,11/9)問2{3^n-3*2^(n-1)+3}/4^n
大問2 3√3/4
大問3 (14+3√3)/13
大問4 2log(√2+1)
大問5 (1)(0,0) (2) x^2+(y+2)^2=4(y>-2)
今年の問題は全体的にかなり易しめだったように思いました。その中でまだ思考力を要するのが大問6の問2だったのではないかと感じました。なので今回は大問6の問2の平均値の定理について細かい解説をブログに書きます。

平均値の定理っぽさに気づけるようになる
この問題は平均値の定理を用いて証明する問題なのですが、このような問題で最も大事なことは平均値の定理で証明することに気づけるようになることです。
実際僕は問題を見た瞬間から平均値の定理っぽいなあという風に感じました。もしこれを読んでくれている人の中でこの問題の平均値の定理っぽさに気づけないとすれば、それは平均値の定理というものへの理解が足りていないのではないかと思います。
平均値の定理とは

平均値の定理とはこの上に書かれているものです。ただこれだけ読んでも僕もイマイチ意味がわからないです。平均値の定理の理解のためにはグラフ上でのイメージを理解する必要があります。
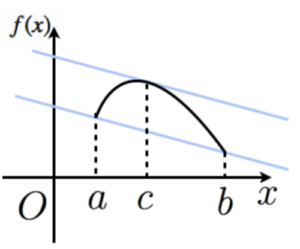

今回の京大数学の問題では「微分可能」という言葉が問題文中にあったり、接線の存在の証明であることからも1とaの範囲で平均値の定理を使う問題なのではないかと予想出来ることがすごく大事な能力となるのです。
今回の平均値の定理の使い方
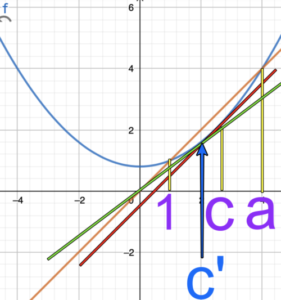
今回の問題で平均値の定理を使うということを考えて使う範囲は1からaなわけですがY=f(x)にそのまま使うとどうなるかという話をすると図のようなcが存在するということになるわけです。ただこのcが存在したところでこの問題ではあまり意味がないわけではないわけです。
なぜならこのcにおける接線(赤い直線は)は原点を通るわけではないので意味がないわけです。
存在証明したい直線は緑の直線なわけです。その接点であるc'の存在をこの問題では証明する必要があります。
Y=f(x)/xを考える理由
今回の問題ではy=f(x)/xという関数を考えられるかで勝負が決まると言っても過言ではありません。ではなぜこの関数を考えようと思えるのでしょうか。
一つはそのままf(x)で平均値の定理を使ってもうまくいかないので別の関数で使おうと思うというのが一つの理由です。ただそれだけでは別にy=f(x)/xである理由にはなりません。
実際には平均値の定理を普通に使ってもうまくいかないときに色々な関数で使おうと思えること自体は非常に大事で、たまたまy=f(x)/xを考えついたというのも一つの能力ではないかと思います。
ただし今回の問題で僕は根拠を持ってy=f(x)/xという関数を考えました。

僕は今回存在証明をしたい緑の直線の特徴を考えました。この直線に特徴的なのは原点とy=f(x)上の点を結んだ直線の傾きが1とaの間では最小であるということです。
今回は1とaの間が下に凸なので最小になるんですが逆に上に凸であれば最大になるわけです。いずれにしても傾きすなわちf(x)/xが極大或いは極小値を取る点こそがc'となるわけなのです。そのためy=f(x)/xという関数で平均値の定理を使えば上手くいきそうだなあと考えたのです。
2021京大理系数学を解いてみて
今年の問題は全体的にかなり平易だったように感じました。もしかしたらコロナの影響で簡単めに問題を作ったのかもしれません。そんな中で最後の問題に関して説明したように自分で新たな関数を考え出すということをしなければ解けない問題であったので差がつく問題だったのではないでしょうか。
平均値の定理は文面だけ読むとよくわからない定理なのですが、図形をイメージすることで理解が深まり、平均値の定理っぽさに気づけるようになると思いますので受験生の方はこの記事を参考に平均値の定理をマスターして頂ければ幸いです。
